- not so Frequently Asked Questions -

1 | 2 |

l=1,m=-1,+1

В квантовой механике значения сферического гармоника Y[lm] l и m являются угловыми моментами и магнитными квантовыми числами. Здесь буде показано несколько сферических гармоников с относительно малым количеством значений l. Метод тот же, что и в предыдущем разделе --- Выражать x,y,z параметрами u и v.

При m нечетном, сферический гармоник содержит мнимую часть exp(-im phi). для m=-1 и 1 функция имеет вид:

   Y[1,-1](t,p) =  sqrt(3/8pi) sin(t) exp(-i p)
   Y[1, 1](t,p) = -sqrt(3/8pi) sin(t) exp( i p)

|Y|^2 легко вычислить, умножив Y и его комплексное сопряжение, и обе, приведенные выше, стали одинаковыми функциями, Y(t)=3/8 pi sin^2(t). Комплексная сопряженная функция сферического гармоника может быть задана соотношением (Y[l,m])^* = (-1)^m Y[l,-m].

gnuplot> set parametric

        dummy variable is t for curves, u/v for surfaces
gnuplot> set angle degree
gnuplot> set urange [0:360]
gnuplot> set vrange [-90:90]
gnuplot> set isosample 36,18
gnuplot> set ticslevel 0
gnuplot> set size 0.65,1.0
gnuplot> a=3.0/(8*pi)
gnuplot> fx(u,v)=cos(u)*cos(v)
gnuplot> fy(u,v)=sin(u)*cos(v)
gnuplot> fz(v)=sin(v)
gnuplot> g(v)=cos(v)*cos(v)
gnuplot> splot a*g(v)*fx(u,v),a*g(v)*fy(u,v),a*g(v)*fz(v)

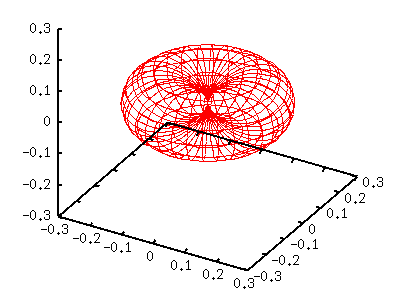
Слева фигура полукруглый фриз ("спасательный круг") |Y[11]|^2. Т.к. функция содержит sin(t)=cos(v), определили g(v)=cos(v)*cos(v) .

l=2,m=-2,-1,0,+1,+2

При l=2, есть 5 различных функций, соответствующих m=-2 до 2.

   Y[2,-2](t,p) =  sqrt(15/32pi) sin(t)sin(t) exp(-2i p)
   Y[2,-1](t,p) =  sqrt(15/8pi) sin(t)cos(t) exp(-i p)
   Y[2, 0](t,p) =  sqrt(5/16pi) (3cos(t)cos(t)-1)
   Y[2, 1](t,p) = -sqrt(15/8pi) sin(t)cos(t) exp( i p)
   Y[2, 2](t,p) =  sqrt(15/32pi) sin(t)sin(t) exp( 2i p)

Здесь показан случай m=0,1,2. Функция с отризательным значением как для m так и для |m|.

m=0

gnuplot> a= 5.0/(16*pi)
gnuplot> g(v)= (3*sin(v)*sin(v)-1)**2
gnuplot> splot a*g(v)*fx(u,v),a*g(v)*fy(u,v),a*g(v)*fz(v)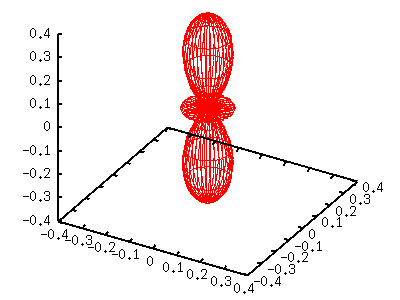

m=1

gnuplot> a=15.0/( 8*pi)
gnuplot> g(v)= (sin(v)*cos(v))**2
gnuplot> splot a*g(v)*fx(u,v),a*g(v)*fy(u,v),a*g(v)*fz(v)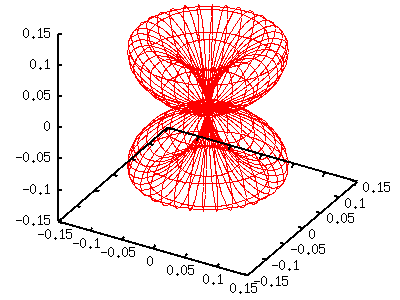

m=2

gnuplot> a=15.0/(32*pi)
gnuplot> g(v)= (cos(v)*cos(v))**2
gnuplot> splot a*g(v)*fx(u,v),a*g(v)*fy(u,v),a*g(v)*fz(v)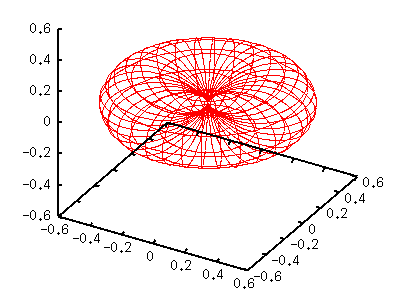