- not so Frequently Asked Questions -
update 2005/11/19
|
|
- not so Frequently Asked Questions - update 2005/11/19
|
Деформация ядра (расширения Лежандра)[ver.4] ONLY ! Сферический гармоник Y[lm](theta,phi) к простой функции Лежандра p[l](cos(theta)) масштабируемый постоянной при m=0, которая не зависит от phi. Следующее уравнение фигуры Y[l](theta) для нескольких значений l.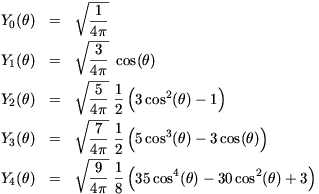 
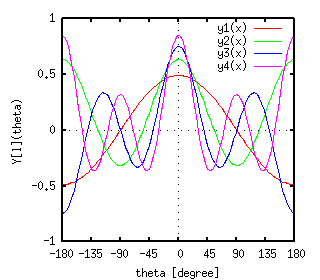
Используя Y[l](theta) с l=lambda=точной части, форма деформирования ядра может быть выражена следующим образом: 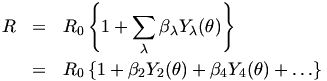 где beta параметр деформации. Если beta=0, ядро сферическое. 3D форма задается уравнением Gnuplot. Как уже было паказано в предыдущем разделе, координаты (x,y,z) выражаются через угол u,v и радиус r. x = R(theta)*cos(u)*cos(v) y = R(theta)*sin(u)*cos(v) z = R(theta)*sin(v) где theta угол до оси Z, так что отношение между theta и v является theta = pi/2-v. Для построения поверхности, параметры u,v варьируются от 0 до 360 градусов. В случае beta_2 = 0.3, beta_4 = 0.1 и R_0 = 1:
gnuplot> set parametric
dummy variable is t for curves, u/v for surfaces
gnuplot> set angle degree
gnuplot> set urange [0:360]
gnuplot> set vrange [0:360]
gnuplot> set isosample 16,16
gnuplot> set ticslevel 0
gnuplot> set view 75,25
gnuplot> set size 0.7,1.0
gnuplot> set xrange [-2:2]
gnuplot> set yrange [-2:2]
gnuplot> set zrange [-2:2]
gnuplot> set urange [0:360]
gnuplot> set vrange [0:360]
gnuplot> y0(t)=1.0
gnuplot> y2(t)=sqrt(5.0/(4*pi))*( 3.0*cos(t)**2 - 1.0 )/2.0
gnuplot> y4(t)=sqrt(9.0/(4*pi))*(35.0*cos(t)**4 - 30*cos(t)**2 +3.0)/8.0
gnuplot> b2=0.3
gnuplot> b4=0.1
gnuplot> r(t) = 1 + b2*y2(0.5*pi-t) + b4*y4(0.5*pi-t)
gnuplot> fx(u,v)=cos(u)*cos(v)
gnuplot> fy(u,v)=sin(u)*cos(v)
gnuplot> fz(v)=sin(v)
gnuplot> set pm3d
gnuplot> splot r(v)*fx(u,v),r(v)*fy(u,v),r(v)*fz(v) with lines
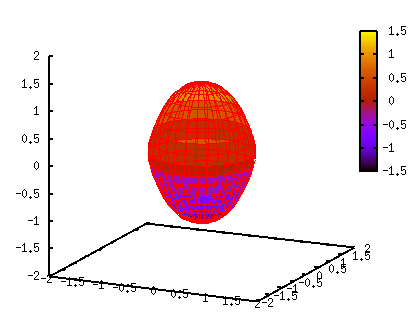 Деформация параметров, beta_2 и beta_4 могут быть положительными и отрицательными. Вот некоторые примеры для некоторых комбинаций beta_2 и beta_4. Параметр beta_2 равен -0.4 или 0.4 и для каждого значения beta_2 изменили значение beta_4 от -0.2 до 0.2. Когда beta_2 положительная, ядро вытянутое, при отрицательном beta_2, ядро сплюснутое. gnuplot> set border 0 gnuplot> unset xtics gnuplot> unset ytics gnuplot> unset ztics gnuplot> unset colorbox gnuplot> b2 = -0.4 ; b4 = -0.2 ; replot ; pause -1 gnuplot> b2 = -0.4 ; b4 = 0.0 ; replot ; pause -1 gnuplot> b2 = -0.4 ; b4 = 0.2 ; replot ; pause -1 gnuplot> b2 = 0.4 ; b4 = -0.2 ; replot ; pause -1 gnuplot> b2 = 0.4 ; b4 = 0.0 ; replot ; pause -1 gnuplot> b2 = 0.4 ; b4 = 0.2 ; replot ; pause -1
 |
