GNUPLOT

- not so Frequently Asked Questions -

update 2004/12/04
HOME | INTRODUCTION | INFORMATION | GALLERY | JAPANESE

Spherical Harmonics

Сферический гармоник в полярных координатах Y[lm](theta,phi) определяется по формуле: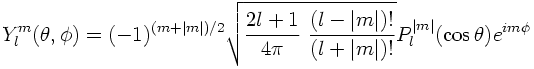

eq

где P[lm] - присоединенная функция Лежандра. Значение l - целое число, l=0,1,2,3... Для каждого значения l, m принимает значение m=-l,-l+1,...l-1,l так что есть 2l+1 различных m значениям. Квадрат это функции нормирован единице, < Y[lm] | Y[l'm'] > = delta(ll') delta(m,m'). Theta пробегает от 0 до pi, а phi пробегает от 0 до 2pi.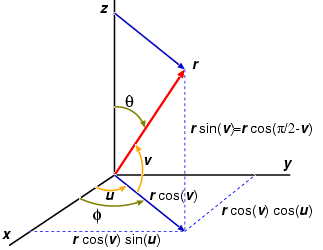


coordinate2

В Gnuplot параметрическое представление угла u такое же как phi, в то время как theta отличается от v. Из левого рисунка theta = pi/2 - v, получим: 

   cos(theta)=sin(v)
   sin(theta)=cos(v)

Простейший сферический гармоник можно получить, прировняв l и m нулю. Это дает постоянное значение 1/sqrt(4pi). Его квадрат |Y[00]|^2=1/4pi тоже постоянен и радиус равен 1/4pi. В Gnuplot легко построить данную функцию. Процедура такая же, как и на предыдущей странице.

gnuplot> set parametric

        dummy variable is t for curves, u/v for surfaces
gnuplot> set angle degree
gnuplot> set urange [0:360]
gnuplot> set vrange [-90:90]
gnuplot> set isosample 36,18
gnuplot> set ticslevel 0
gnuplot> set size 0.65,1.0
gnuplot> a=1.0/(4*pi)
gnuplot> fx(u,v)=cos(u)*cos(v)
gnuplot> fy(u,v)=sin(u)*cos(v)
gnuplot> fz(v)=sin(v)
gnuplot> splot a*fx(u,v),a*fy(u,v),a*fz(v)
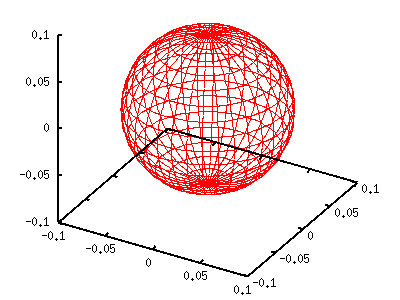
sph00

На левом графике квадрат Y[00], с центром в начале координат и радиусом 1/4pi. Т.к. m=0, часть exp(-im phi) исчезает и функция не зависит от phi. Сферический гармоник становиться реальным, когда m четное. Если m нечетная, то функция имеет мнимую часть.


Далее рассмотрим случай l=1 и m=0. Эта функция определяется Y(theta)=sqrt(3/4pi)cos(theta). Как показанно выше, cos(theta) задается sin(v). Функция может быть построена, когда координаты x,y,z умножаются на sin(v). В следующем примере будет показано |Y[10]|^2=3/4pi cos^2(theta).

gnuplot> a=3.0/(4*pi)
gnuplot> g(v)=sin(v)*sin(v)
gnuplot> splot a*g(v)*fx(u,v),a*g(v)*fy(u,v),a*g(v)*fz(v)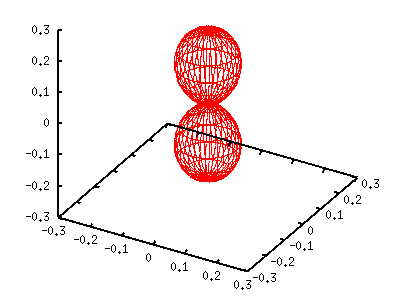
sph10

Сечения сферического гармоника можно увидеть, установив диапазон u [0:180] и использовав опцию hidden3d . 

gnuplot> set urange [0:180]
gnuplot> set hidden3d
gnuplot> splot a*g(v)*fx(u,v),a*g(v)*fy(u,v),a*g(v)*fz(v)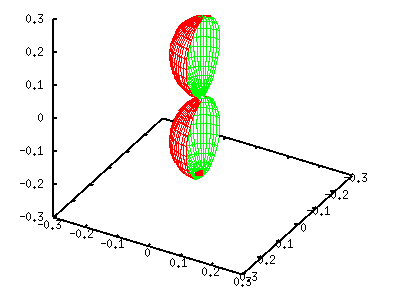
sph10
from Dr.Nakamura of TUS. Thanks !
up