Фрактал

• Рекурсивность
• Множество Мандельброта
• Множество Жюлиа

Множество Жюлиа

То же, что и множество Мандельброта. Вычисляем рекуррентное отношение комплексной переменной A, и смотрим для каких чисел значения |z(n)|^2 не расходятся для большого числа n. Отличия от множества Мандельброта в том, что начальное значение рекуррентного отношения координат (x,y) на комплексной плоскости и значение A произвольно.

    z(0)   = X + iY
    z(n+1) = z(n)*z(n) + A

Функция расчета функции представленая выше, такая же как и функци mandel в предыдущем разделе. Комплексное значение A Дается за пределами функции и координаты (X,Y) используются как начальные значения. Здесь используем A=-0.37-0.612 i.

gnuplot> set xrange [-0.5:0.5]
gnuplot> set yrange [-0.5:0.5]
gnuplot> set logscale z
gnuplot> set isosample 50
gnuplot> set hidden3d
gnuplot> set contour
gnuplot> a= -0.37
gnuplot> b= -0.612
gnuplot> splot mandel(a,b,complex(x,y),0) notitle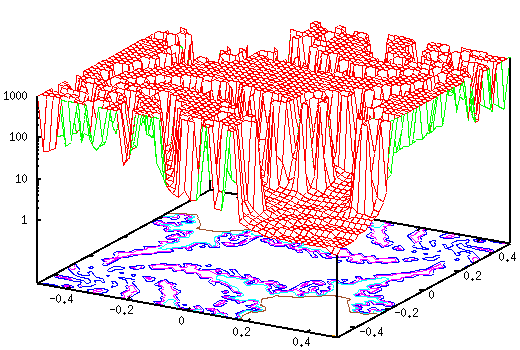

Можно сделать великое множество образов, изменяякомплексную постоянную A. В самом деле, очень маленькое изменение в постоянной дает совершенно другую картину. Например, значения A были -0.37 -0.612 i на фигуре выше, но если изменить мнимую часть до 0.6, то получится: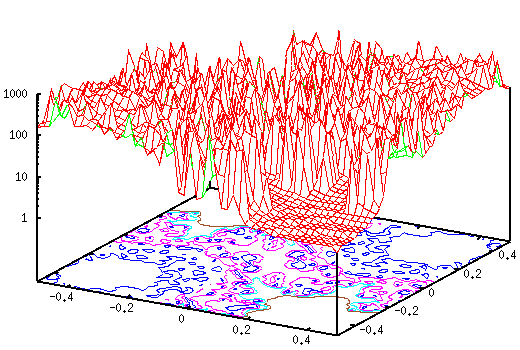

Следующие CGs фракталы были сделаны параметрами приведенными выше.