Фрактал

• Рекурсивность
• Множество Мандельброта
• Множество Жюлиа

Рекурсивность

Можно определить функцию рекурсивно, для этого необходимо включить функцию саму в себя. Например, факториал целого числа N!=FAC(N) записывается как FAC(N)=N*FAC(N-1),в gnuplot определяется как:

gnuplot> fac(n) = n * fac(n-1)

Эта функция бесконечного цикла, в котором переменная N уменьшается на 1. Для прекращения цикла используется тройной оператор. Следующий пример говорит остановить цикл при N=0.

gnuplot> fac(n) = (n==0) ? 1 : n * fac(n-1)

Это означает, что когда N равно 0 сразу после '?' подсчитывается, в противном случае выполняется fac(n-1), и снова, та же функция, но ее аргумент равен n-1. Вызов функции прекращается при значении аргмента равном нулю.

Для расчета N!, N должно быть целым числом. Если аргумент действительное число, используем функцию int(), преобразуя в целое число. Возможно стоит так же включить ограничение, что N должно быть положительным, хотя это не обязательно.

gnuplot> fac(x) = (int(x)==0) ? 1.0 : int(x) * fac(int(x)-1.0)

Теперь можно вычислить функцию fac(x), следующим образом:

gnuplot> fac(x) = (int(x)==0) ? 1.0 : int(x) * fac(int(x)-1.0)
gnuplot> print fact(1)
1.0
gnuplot> print fact(5) 
120.0
gnuplot> print fact(5.5) 
120.0
gnuplot> print fact(20) 
2.43290200817664e+18

Известно, что N! может быть аппроксимирована формулой Стирлинга.

Сравним формулу Стирлинга с функцией fac(x).

gnuplot> stirling(x) = sqrt(2*pi*x) * x**x * exp(-x)
gnuplot> set xrange [1:15]
gnuplot> set yrange [1:1e+10]
gnuplot> set log y
gnuplot> set sample 15
gnuplot> plot stirling(x) notitle with lines,\
>             fact(x)     notitle with points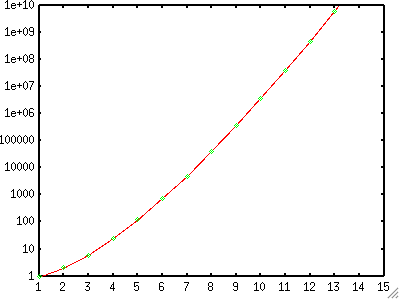