Фрактал

• Рекурсивность
• Множество Мандельброта
• Множество Жюлиа

Множество Мандельброта

Имеем комплексное значение A, вычислим следующее рекуррентное отношение. Если |z(n)|^2 не расходятся, когда n становиться очень большим числом, комплексное значение A принадлежит множеству Мандельброта.

    z(0)   = 0.0
    z(n+1) = z(n)*z(n) + A

Будем считать, что плоскость XY - комплексная плоскость и точка A определена на ней. Расчитаем рекуррентное отношение, показанное выше, и если значение |z|^2 начинаетрасходиться на определенное количество интеграций n, дадим числу n значение точки Z(X,Y). Можно построить 3D изображение множества Мандельброта с теми данными (X,Y,Z). Сначала определим рекуррентное отношение, как рекурсивную функцию. Эта функция возвращает число интеграций n, когда |z|^2 становиться больше некоторого вещественного числа (в данном случае 2). Верхний предел интеграций равен 1000, необходимый для избежания бесконечного цикла.

В Gnuplot комплексное значение z, чья действительная часть a и мнимая b написано как z={a,b}. Функция real(z) и imag(z) возвращают действительную и мнимую части соответственно. Абсолютное значение z - abs(z). С другой стороны, нетпростого способа получить комплексное значение из действительного, определим новую функцию: complex(x,y)=x*{1,0}+y*{0,1}.

complex(x,y) = x*{1,0}+y*{0,1}
mandel(x,y,z,n) = (abs(z)>2.0 || n>=1000) ? \
                  n : mandel(x,y,z*z+complex(x,y),n+1)

Координаты x,y являются значением A на комплексной плоскости. Функция Мандель расчитывается z^2+A, и когда ее абсолютное значение превышает 2.0, функция возвращает число интеграций, n. При вызове этой функции необходимо дать начальные значения z и n равные {0,0} и 0 в дополнение к значениям x и y.

gnuplot> set xrange [-1.5:0.5]
gnuplot> set yrange [-1:1]
gnuplot> set logscale z
gnuplot> set isosample 50
gnuplot> set hidden3d
gnuplot> set contour
gnuplot> splot mandel(x,y,{0,0},0) notitle

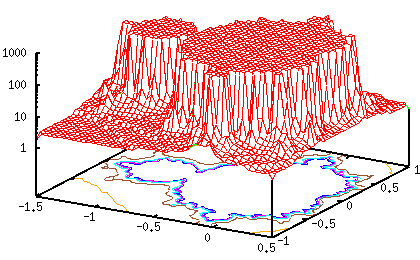
В компьютерной графике часто можно увидеть хорошие графики множества Мандельброта. Чтобы сделать такое изображение, Выделяют каждый пиксель изображения на определеные точки комплексной плоскости, и вычисляют пиксельное рекуррентное отношение. При расхождении вычислений, пиксель принимает цветную точку, цвет изменяется с числом интеграций. Здесь построили 2D изображение Мандельброта Mandelbrot с простым X Window программы . Плато на графике соответсвует черный участок в правом изображении.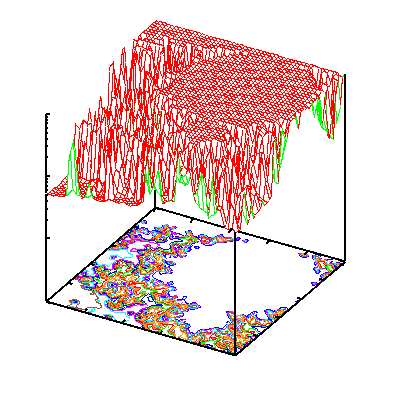

Как можно увидеть на изображении слева, структура увеличенного множества Мандельброта очень сложна. Эти фрактальные изображения были показаны с помощью очень тонких линий контура, однако, Gnuplot делает их не так хорошо как игры с компьтерной графикой. Новая версия Gnuplot, version 3.8, может построить лучше цвета для 3D графика.

Вот некоторые CGs сделанные в системе X Window игрушкой программы.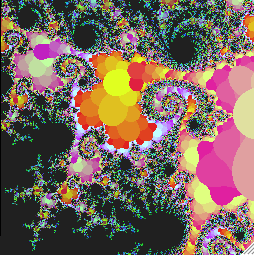