-не так Часто Задаваемые Вопросы - update 2010/12/26
|
|
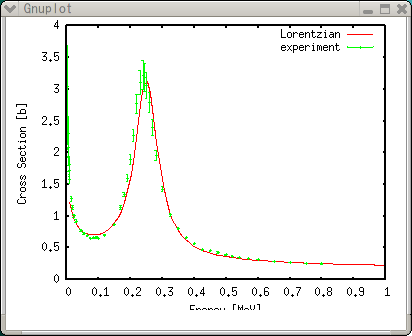
Введение в Gnuplot - ФункцииФункции определяемые пользователемЕсли вы зададите уравнение, gnuplot вычислит его корни. Это означает, что функции могут быть построены только после преобразования в простейшую форму. Например, функция f(x)=a*x+b не содержит сложных интегральных или дифференциальных значений, которые нужно вычислять. Gnuplot позволяет строить графики элементарных функций и специальных функций (синуса, косинуса, Бесселя и т.д.). Gnuplot может решать не только линейные уравнения наименьших квадратов, но также и нелинейные. В этом параграфе мы рассмотрим, как можно использовать определенную пользователем функцию, и как применить к ней экспериментальные данные. Рассмотрим, например, функцию Лоренца плюс значение 1/sqrt(x). Это уравнение содержит четыре параметра, a, b, c, и d, которые задаются экспериментальными данными. 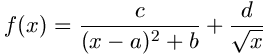 Синтаксис задания функции схож с объявлением в языках программирования Fortran или C. В примере ниже f(x)=c/((x-a)*(x-a)+b)+d/sqrt(x) определяет наше уравнение. Квадрат (x-a) может быть записан как на языке Fortran, (x-a)**2 . Параметры a,b,c, и d произвольны. gnuplot> a=0.25 gnuplot> b=0.02 gnuplot> c=0.05 gnuplot> d=0.1 gnuplot> f(x)=c/((x-a)*(x-a)+b)+d/sqrt(x) gnuplot> set xrange [0:1] gnuplot> set yrange [0:4] gnuplot> plot f(x) 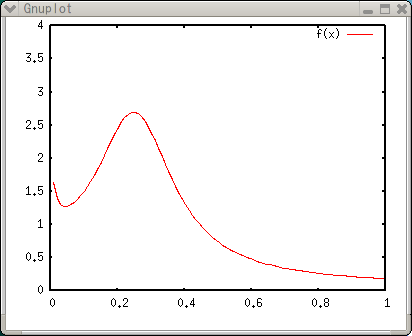 Значения функцийТак как gnuplot вычисляет определенные пользователем функции численно, то чтобы построить график, нужно просмотреть вычисленные значения с помощью команды print. Значения функции зависят от параметров (a,b,c,d, e). Gnuplot производит вычисления с двойной точностью. gnuplot> print f(0.25) 2.7 gnuplot> print f(0.4) 1.33458447124371 gnuplot> a=0.4 gnuplot> print f(0.4) 2.65811388300842 Для получения значений в табличном виде, которые могут быть обработан с помощью других приложений, таких как a spread-sheet, используется специальный терминал table. Чтобы записать результат в заданный файл используйте set output. gnuplot> set term table Terminal type set to 'table' gnuplot> plot f(x) #Curve 0, 100 points #x y type 0 0 u 0.010101 1.63972 i 0.020202 1.39031 i 0.030303 1.30688 i .... 0.979798 0.191506 i 0.989899 0.188622 i 1 0.185837 i gnuplot> set output "calc.plt" gnuplot> replot Поиск параметров методом наименьших квадратовТеперь применим к функции экспериментальные данные и получим значения параметров a, b, c и d. Экспериментальные данные сохранены в файле "exp.dat". 2.5000E-03 3.0420E+00 6.47E-01 3.5000E-03 2.5700E+00 4.37E-01 4.5000E-03 2.3020E+00 2.53E-01 ... 7.0000E-01 2.7420E-01 2.14E-03 7.5000E-01 2.5680E-01 1.81E-03 8.0000E-01 2.4630E-01 1.59E-03 Файл данных содержит 3 колонки, каждая из которых тройка данных (x,y,z), данные Z являются абсолютной погрешностью данных Y. Это означает, что Z имеет такую же размерность, что и Y. Например,( в случае выше), если значение Y - 3.04 cm, то её погрешность должна быть 0.647cm. Если погрешность не задана, то значение задаётся для всех одно и то же. gnuplot> set xlabel "Energy [MeV]" gnuplot> set ylabel "Cross Section [b]" gnuplot> set xtics 0.1 gnuplot> set ytics 0.5 gnuplot> plot f(x) title "Lorentzian",\ > "exp.dat" using 1:2:3 title "experiment" with yerrors 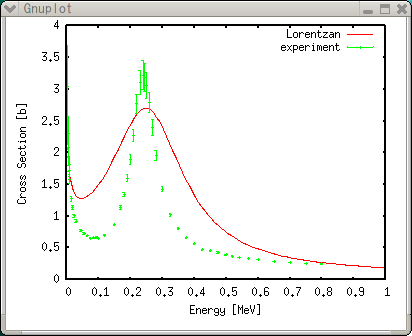
Параметры a,b,c, и d произвольны, но они определяются примерно для этих экспериментальных данных. Параметр 'a' это позиция вершины Лоренцевой функции, который примерно равен 0.25 из построения. Квадратный корень параметра 'b', отвечает за ширину вершины, и его значение можно выбрать примерно равным 0.02. Довольно легко сделать подбор методом наименьших квадратов с помощью gnuplot. Используйте команду fit и добавьте параметры, которые нужно найти опцией via. Когда ваша функция строго нелинейна, вы должны быть осторожны в определении значений параметров. Здесь мы использовали значения выше в качестве начальных параметров для этой подстановки.
gnuplot> fit f(x) "exp.dat" using 1:2:3 via a,b,c,d
Iteration 0
WSSR : 96618.1 delta(WSSR)/WSSR : 0
delta(WSSR) : 0 limit for stopping : 1e-05
lambda : 1150.73
initial set of free parameter values
...
After 17 iterations the fit converged.
final sum of squares of residuals : 3341.93
rel. change during last iteration : -5.29173e-06
degrees of freedom (ndf) : 47
rms of residuals (stdfit) = sqrt(WSSR/ndf) : 8.43237
variance of residuals (reduced chisquare) = WSSR/ndf : 71.1049
Final set of parameters Asymptotic Standard Error
======================= ==========================
a = 0.26191 +/- 0.005759 (2.199%)
b = 0.00251445 +/- 0.0008358 (33.24%)
c = 0.00541346 +/- 0.0009206 (17.01%)
d = 0.182469 +/- 0.007329 (4.016%)
correlation matrix of the fit parameters:
a b c d
a 1.000
b 0.042 1.000
c -0.229 0.783 1.000
d 0.210 -0.538 -0.768 1.000
gnuplot> replot
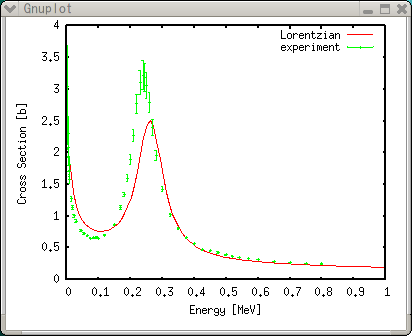 Как показано выше, аппроксимационная функция не настолько хороша, за исключением области резонанса. Это из-за того, что функция была подобрана неправильно. Форма её вершины похожа на форму вершины функции Лоренца, поэтому мы изменяем d/sqrt(x), вводя новый параметр 'e', и выражаем его как d*x**e. Начальное значение 'e'-0.5.
gnuplot> e=-0.5
gnuplot> f(x)=c/((x-a)*(x-a)+b)+d*x**e
gnuplot> fit f(x) "exp.dat" using 1:2:3 via a,b,c,d,e
...
Final set of parameters Asymptotic Standard Error
======================= ==========================
a = 0.25029 +/- 0.002106 (0.8412%)
b = 0.00197707 +/- 0.0002747 (13.89%)
c = 0.00550098 +/- 0.0003662 (6.657%)
d = 0.21537 +/- 0.003743 (1.738%)
e = -0.358371 +/- 0.0115 (3.208%)
correlation matrix of the fit parameters:
a b c d e
a 1.000
b 0.021 1.000
c -0.078 0.788 1.000
d -0.110 -0.384 -0.500 1.000
e -0.304 0.198 0.335 0.381 1.000
gnuplot> replot
Вывод в формате PostscriptКак показано в разделе Экспериментальные данные, мы построили график в Postscript. Точки данных нарисованы с помощью сплошной линии и кругов, а функция показана жирной пунктирной линией. gnuplot> set linestyle 1 lt 1 pt 7 gnuplot> set linestyle 2 lt 2 lw 3 gnuplot> set size 0.6,0.6 gnuplot> set term postscript eps enhanced color Terminal type set to 'postscript' Options are 'eps enhanced color dashed defaultplex "Helvetica" 14' gnuplot> set output "exp.ps" gnuplot> plot"exp.dat" using 1:2:3 title "experiment" with yerrors ls 1,\ > f(x) title "Lorentzian" with line ls 2 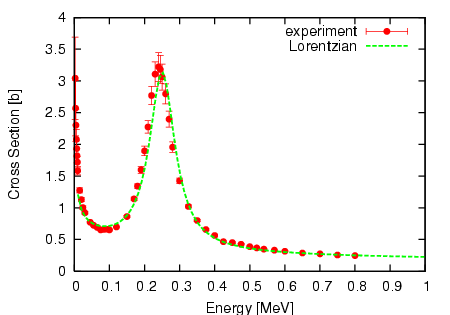 |