Введение в Gnuplot

• Основы
• Числовые данные
• Экспериментальные данные
  • Файл данных
  • Построение
  • Легенда
  • Вычисляемая линия
  • Вид линии
  • Названия осей
  • Диапозон
  • Деления
  • Файл Postscript
• Функции
• Применение gnuplot'a в жизни
• Стилевые тонкости

Введение в Gnuplot - Экспериментальные данные

Приготовление файла данных

Здесь мы описываем, как подготовить экспериментальные данные в файле с данными. В нашем примере есть три набора данных, которые записаны последовательно в файле. Каждй блок данных разделён двумя пустыми линиями. Погрешность задана как абсолютная. Z имеет ту же размерность что и значения Y. Строка, начинающаяся с "#", является комментарием и пропускается.

# Data No. 1
 2.1500E-02 1.3060E+00 5.3098E-02
 2.3900E-02 1.2220E+00 4.7043E-02
 2.6800E-02 1.3430E+00 4.9854E-02
 2.9700E-02 1.2580E+00 4.5860E-02
 3.2500E-02 1.2430E+00 4.4506E-02
               ....
 9.4500E-01 1.2290E+00 3.7317E-02
 1.0350E+00 1.2630E+00 4.1449E-02
 1.1330E+00 1.2670E+00 4.2289E-02


# Data No. 2
 2.4000E-02 1.2970E+00 3.1387E-02
 4.0000E-02 1.3060E+00 2.8993E-02
 6.0000E-02 1.2960E+00 2.8382E-02
 8.0000E-02 1.3300E+00 2.8728E-02
              ....
 7.0000E+00 1.2210E+00 2.5031E-02
 7.2000E+00 1.1990E+00 2.5299E-02
 7.4000E+00 1.1860E+00 2.5618E-02


# Data No.3
 2.2500E-02 1.3310E+00 3.4606E-02
 2.7500E-02 1.3370E+00 2.4066E-02
 3.5000E-02 1.3440E+00 2.6880E-02
              ....
 1.8936E+01 1.0080E+00 2.9232E-02
 2.0064E+01 9.6300E-01 2.9853E-02
 2.1296E+01 1.0310E+00 3.1961E-02

Построение

Эти три набора экспериментальных данных могут быть округлённы с помощью фукнции y = -0.01687 x + 1.3512. Эта функция построится вместе с данными, которые сохранены в файле plotexp.dat. Чтобы получить доступ к каждому блоку данных в файле данных, используйте index ключевое слово , чтобы определить блок, который должен быть построен. Вы можете определить первый блок с помощью index 0:0 или index 0 . Третий блок обозначается как index 2. Чтобы совместит первый и второй блоки, используйте index 0:1 .

Чтобы построить данные с погрешностями, используйте with yerrorbars . Третья колонка отвечает за погрешность и может быть указана с помощью команды using 1:2:3 . Если погрешность задана в процентах (%), используйте using 1:2:($2*$3/100.0) чтобы перевести в абсолютную погрешность.

gnuplot> plot "plotexp.dat" index 0:0 using 1:2:3 with yerrorbars,\
> "plotexp.dat" index 1:1 using 1:2:3 with yerrorbars,\
> "plotexp.dat" index 2:2 using 1:2:3 with yerrorbars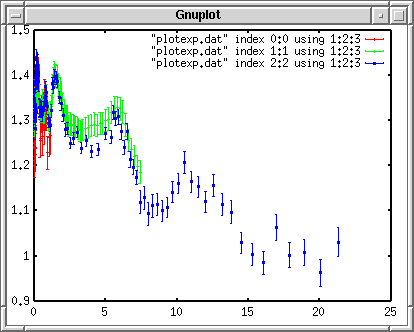

Когда ваша строка слишком длинная, то в её конец помещается символ "\" и тогда следующая строка рассматривается как продолжение предыдущей. Gnuplot работает к сокращениями, например, "w" - "with", "i" - "index", и т.д. Кроме того, вы можете опустить имя файла, если тот же самый файл используется, точно так же как пример выше. В других строках после первой команды "plot" может быть использована краткая форма "" вместо "plotexp.dat".

Создание легенды

Каждый набор экспериментальных данных был измерен тремя различными экспериментаторами. Их имена: "A. Smith" - 1, "B. Smith" - 2, "C. Smith" - 3, и проводили их в 1992, 1993 и в 1999.

gnuplot> plot "plotexp.dat" ind 0:0 usi 1:2:3 ti "A. Smith (1992)" w yerr,\
> "plotexp.dat" ind 1:1 usi 1:2:3 ti "B. Smith (1993)" w yerr,\
> "plotexp.dat" ind 2:2 usi 1:2:3 ti "C. Smith (1999)" w yerr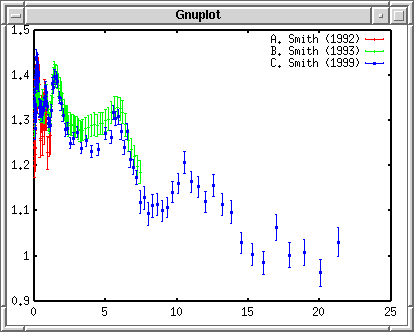

Рисуем вычисляемую линию

Чтобы применить экспериментальные данные к функции, подставим их в линейную функцию, f(x) = -0.01687*x +1.3512, которую сначала нужно определить.

gnuplot> f(x)= -0.01687*x + 1.3512
gnuplot> plot f(x) with lines, \
> "plotexp.dat" ind 0:0 usi 1:2:3 ti "A. Smith (1992)" w yerr,\
> "plotexp.dat" ind 1:1 usi 1:2:3 ti "B. Smith (1993)" w yerr,\
> "plotexp.dat" ind 2:2 usi 1:2:3 ti "C. Smith (1999)" w yerr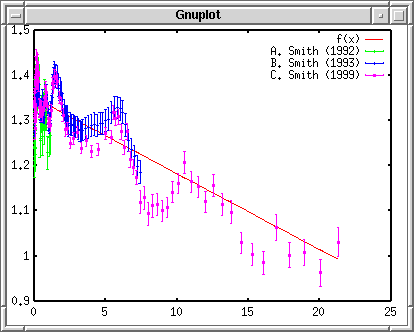

В случае выше, для каждой функции используется разный цвет.

Изменяем вид линии

Графики этих экспериментальных данных различаются цветами, когда построены и показаны вам в отдельном окне. Однако, если их сконвертировать в формат Postscript, то вы увидите странный символ, показанный ниже. В терминале Postscript сплошная линия обозначается номером 1, номера 2,3 и 4 пунктирные и точечные. Поэтому погрешность будет показана как пунктирная линия.

Определим все линии как сплошные и каждому измерению поставим свой символ.

gnuplot> set linestyle 1 lt 1 lw 3
gnuplot> set linestyle 2 lt 1 pt 7
gnuplot> set linestyle 3 lt 1 pt 8
gnuplot> set linestyle 4 lt 1 pt 9

Если ваша версия gnuplot новее чем 3.8:

gnuplot> set style line 1 lt 1 lw 3
gnuplot> set style line 2 lt 1 pt 7
gnuplot> set style line 3 lt 1 pt 8
gnuplot> set style line 4 lt 1 pt 9

Первая строка определяет вид линии No.1 как сплошную с толщиной в 3 пункта. Со второй по четвёртную линий для экспериментальных данных: вид линии - сплошная, а символы - No. 7, 8 и 9.

gnuplot> f(x)= -0.01687*x + 1.3512
gnuplot> plot f(x) notitle with lines linestyle 1, \
> "plotexp.dat" ind 0:0 usi 1:2:3 ti "A. Smith (1992)" w yerr linestyle 2,\ 
> "plotexp.dat" ind 1:1 usi 1:2:3 ti "B. Smith (1993)" w yerr linestyle 3,\
> "plotexp.dat" ind 2:2 usi 1:2:3 ti "C. Smith (1999)" w yerr linestyle 4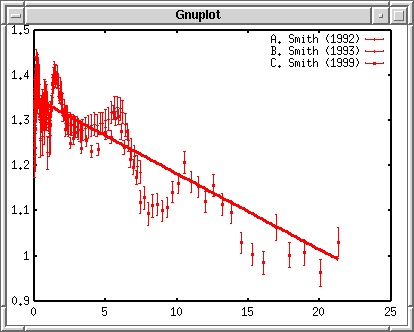

Вставляем названия осей

В графике выше, легенда для графика с подставленными значениями удалена командой notitle. Трудно различать графики, т.к. и линии и точки красного цвета.

Теперь сделаем подписи к осям X и Y. Название оси X - "Energy [MeV]", а название оси Y - "Cross Section [b]". Установим названия с помощью команд set xlabel и set ylabel. Команда replot помогает избежать повторного ввода длинной строки с разными опциями и просто перестраивает график.

gnuplot> set xlabel "Energy [MeV]"
gnuplot> set ylabel "Cross Section [b]"
gnuplot> replot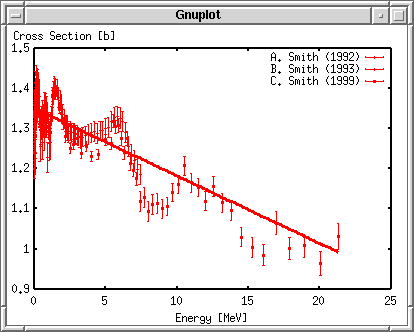

Определеяем диапозон

Теперь определим диапозоны осей X и Y. Для оси Y, установим диапозон от 0 до 2. Рядом с X=0 попадает слишком много значений, поэтому мы воспользуемся логарифмической шкалой чтобы их разделить. Диапозон оси X зададим такой: от 0.01 до 20. Комада set logscale {x|y} установит логарифмическую шкалу.

gnuplot> set xrange [0.01:20]
gnuplot> set yrange [0:2]
gnuplot> set logscale x
gnuplot> replot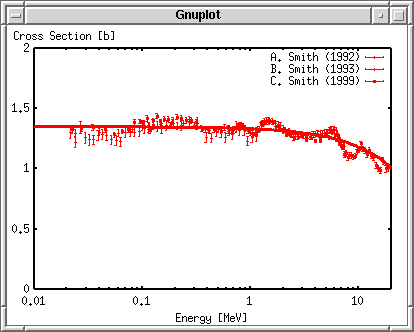

Устанавливаем деления

Устанавливаем деления на осях. Ось X логарифмическая, поэтому оставим её. Ось Y имеет деления с интервалом 0.5. Установим интервал равный 1 и поделим его на 10 частей. В дополнение к этому нарисуем сетку под графиком. Сетка показывает пересечение значений основных делений.

gnuplot> set ytics 1
gnuplot> set mytics 10
gnuplot> set grid
gnuplot> replot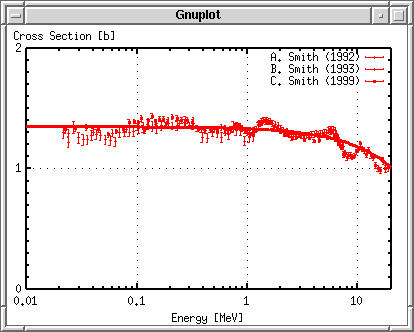

Создаём файл Postscript

С помощью драйвера Postscript определите имя сохраняемого файла, выполните команду replot и вы получите график в формате Postscript. Перед тем как выйти из gnuplot, сохраните всё в какой-нибудь файл.

gnuplot> set term postscript
gnuplot> set output "plotexp.ps"
gnuplot> replot
gnuplot> save "plotexp.plt"
gnuplot> quit

Принтер Postscript может печатать графики. Просмотрщики Postscript такие как ghostscript или gv могут показать содержимое файлов.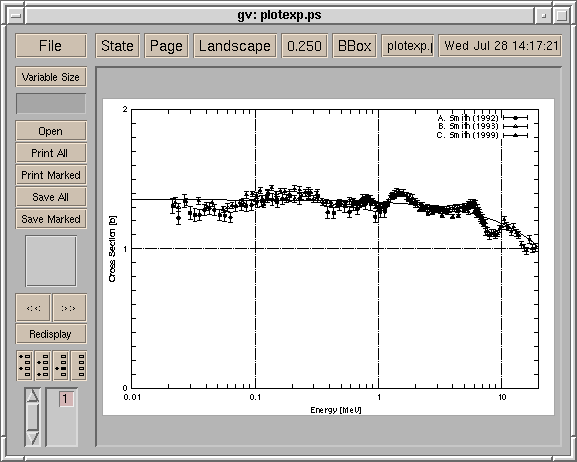

Очень трудно что-то понять, т.к. изображение очень маленькое. В любом случае символ No.7 - закрашеный круг, No.8 - пустой треугольник, No.9 - закрашенный треугольник. Типы символов и линий зависят от терминалов. Существует много символов, которые использует терминал Postscript, но их число ограничено для использования при построении по экспериментальным данным. Ниже приведён список символов: symbols.