GNUPLOT

-не так Часто Задаваемые Вопросы-

обновлено 2010/12/26
Домашняя страница | Введение | Информация | Галерея | Японский | Английский

Разное (No.2)

1 | 2 | 3 | 4

Приближение нелинейной функции методом наименьших квадратов (I)

В gnuplot 3.7 включено условие приближения к среднеквадратичному. Оно производит автоматический поиск параметров произвольной функции путем интеграции данных в файл. Функция может быть линейной или нелинейной, но она должна быть выражена форматом gnuplot. Пример приближения данных, соответствующий Лоренцевой функции f(x)=a/(1+b*x*x). Переменные a и b - параметры.

Данные, приведенные в пример, были получены при значениях a=2 и b=1, чтобы показать, что gnuplot дает правильный ответ.

-10.000000    0.019802
 -8.947370    0.024674
 -7.894740    0.031582
 -6.842110    0.041828
 -5.789470    0.057941
 -4.736840    0.085333
 -3.684210    0.137236
 -2.631580    0.252359
 -1.578950    0.572561
 -0.526316    1.566160
  0.526316    1.566160
  1.578950    0.572561
  2.631580    0.252359
  3.684210    0.137236
  4.736840    0.085333
  5.789470    0.057941
  6.842110    0.041828
  7.894740    0.031582
  8.947370    0.024674
 10.000000    0.019802

Эти значения хранятся в файле данных "exp.dat". Сначала, приближается функция, которая определена. Параметры поиска являются произвольными, за исключением "x" или "t", которые используются gnuplot. Данные начинают приближаться командой fit. Имена параметров задаются опцией via.

Для приближения данных используются опции using, index, every Неопределенные точки данных рассматриваются так же, как и все его значения. Если точка данных имеет погрешность sigma, значение становиться равным sigma^{-2}. Для значений приближенных к среднеквадратичным, погрешности обрабатываются в третьей колонке файла данных, в которой необходимо указать, какие неопределенны, как например fit f(x) "exp.dat" using 1:2:3 via a,b. Если погрешности данных не указанны, все точки данных имеют одинаковые значения.

gnuplot> f(x)=a/(1+b*x*x)  
gnuplot> fit f(x) "exp.dat" via a,b


Iteration 0
WSSR        : 1.43879           delta(WSSR)/WSSR   : 0
delta(WSSR) : 0                 limit for stopping : 1e-05
lambda      : 0.201184

                         .......

Final set of parameters            Asymptotic Standard Error
=======================            ==========================

a               = 2                +/- 5.236e-07    (2.618e-05%)
b               = 0.999998         +/- 7.397e-07    (7.397e-05%)


correlation matrix of the fit parameters:

               a      b      
a               1.000 
b               0.837  1.000

Во время приближения данных, можно просматривать изменения параметров на дисплее. Эти же данные можно найти в файле "fit.log", который создается в текущем каталоге. Если все было выполнено правильно, то будут получены окончательные значения параметров, вместе с ковариантной матрицей. В приведенном выше примере были получены правильные параметры a=2 и b=1.

Окончательные результаты хранятся в переменных a и b, так что можно сравнить подобранные функции и данные, путем построения с заданными параметрами. 

gnuplot> plot f(x) with lines, "exp.dat" using 1:2 w points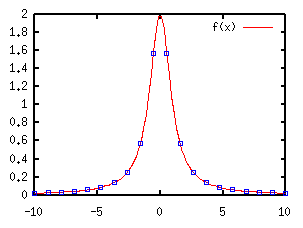
fig/sample9.3
up

Приближение нелинейной функции методом наименьших квадратов (II)

Следующий пример является более реалистичным. Есть экспериментальные данные, показанные ниже. В функцию f(x)=c*(x-a)**b подбираются данные путем вычисления переменных a, b и c.

# X        Y     Z
  6.295    8.4   0.3
  6.795   23.9   0.7
  7.826  104.0   3.0
  8.830  255.0   8.0
  9.841  421.0  13.0
 10.860  566.0  18.0
 11.864  690.0  22.0

Каждая точка имеет погрешности (Z), тогда весовые коэфициенты точек равны 1/Z*Z.

В начале построение экспериментальных данных видно только тенденцией.

gnuplot> set log y
gnuplot> plot "exp.dat" using 1:2:3 w yerrorbars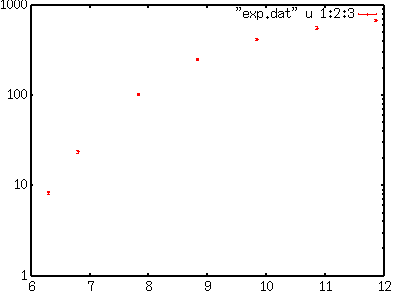
fig/sample9.4a

Далее, выбираются начальные значения этих переменных a, b и c. Если начальные значения не указаны, gnuplot предполагает, что они равны 1. Так как это значения в некоторых случаях является недостаточным, необходимо задать лучшие начальные координаты. Приближение функции f(x)=c*(x-a)**b, как можно догадаться, происходит при значении a в районе 6, потому что f(x)=0 при x=a, c кратно 10 (См. log(f(x))) и b равно 1 или 2, а f(x) принимает значения от 10 до 100 раз, когда x увеличивается на 1. Эти значения используются для начальных.

gnuplot> a=6
gnuplot> b=1
gnuplot> c=10
gnuplot> f(x)=c*(x-a)**b
gnuplot> fit f(x) "exp.dat" using 1:2:3 via a,b,c

Вычисления сходятся после 17 интеграций, конечные значения отображаются вместе с ковариационными. Полученные значения a=5.77, b=1.89, c=25.8. 

After 17 iterations the fit converged.
final sum of squares of residuals : 90.8196
rel. change during last iteration : -9.71916e-09

degrees of freedom (ndf) : 4
rms of residuals      (stdfit) = sqrt(WSSR/ndf)      : 4.76497
variance of residuals (reduced chisquare) = WSSR/ndf : 22.7049

Final set of parameters            Asymptotic Standard Error
=======================            ==========================

a               = 5.76731          +/- 0.176        (3.051%)
b               = 1.89369          +/- 0.2127       (11.23%)
c               = 25.7956          +/- 9.807        (38.02%)


correlation matrix of the fit parameters:

               a      b      c      
a               1.000 
b              -0.944  1.000 
c               0.975 -0.975  1.000

Эти результаты были составлены экспериментальными данными.

gnuplot> plot f(x),"exp.dat" using 1:2:3 w yerrorbars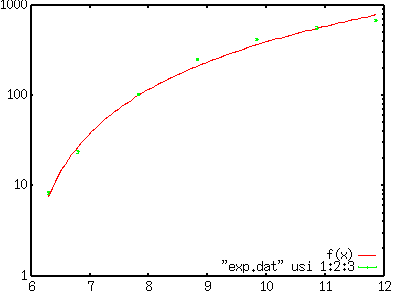
fig/sample9.4b
up